
La configuración electrónica se refiere a la disposición de los electrones alrededor del núcleo de un átomo en su estado fundamental.
El estado en el que todos los electrones del átomo existen en el nivel de energía más bajo posible.
Los diferentes niveles de energía ocupados por los electrones a menudo se denominan capas que rodean el núcleo del átomo.
Por otra parte, cada capa está designada por un número entero, comenzando con 1.
Cuanto mayor sea el número de la capa, mayor será su distancia del núcleo del átomo.
La configuración electrónica de una especie atómica neutra o iónica
Nos permite comprender la forma y energía de sus electrones.
Se tienen en cuenta muchas reglas generales al asignar la «ubicación» del electrón a su estado energético prospectivo.
Sin embargo, estas asignaciones son arbitrarias y siempre es incierto qué electrón se está describiendo.
Conocer la configuración electrónica de una especie nos permite comprender mejor:
- Su capacidad de unión.
- Magnetismo.
- Y otras propiedades químicas.
La configuración electrónica y los números cuánticos
Número cuántico principal (n)
El número cuántico principal n indica la capa o nivel de energía en el que se encuentra el electrón.
El valor de n se puede ajustar entre 1 a n.
- Donde n es el valor de la capa más externa que contiene un electrón.
- Este número cuántico solo puede ser positivo.
- Distinto de cero.
- Y valores enteros.
Es decir, n = 1,2,3,4, ..
- Por ejemplo, un átomo de yodo tiene sus electrones más externos en el orbital 5p.
- Por lo tanto, el número cuántico principal para el yodo es 5.
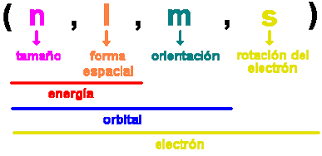
Número cuántico de momento angular orbital (l)
El número cuántico del momento angular orbital, l, indica la subcapa del electrón.
También puede saber la forma del orbital atómico con este número cuántico.
Una subcapa s corresponde a l = 0.
- La primera subcapa p = 1.
- Una subcapa d = 2.
- Otra subcapa f = 3.
- Y, así sucesivamente.
- Este número cuántico solo puede ser valores positivos y enteros.
- Aunque, puede tomar un valor cero.
En general, para cada valor de n, hay n valores de l.
- Además, el valor de, l varía de 0 a n-1.
- Por ejemplo, si n = 3, l = 0, 1, 2.
- Entonces, en lo que respecta al ejemplo usado anteriormente.
- Los valores l de yodo para n = 5 son l = 0, 1, 2, 3, 4.
Número cuántico magnético (m l)
El número cuántico magnético, m l , representa los orbitales de una subcapa determinada.
- Para un l dado, m l puede oscilar entre -l y + l.
- Una subcapa p (l = 1), por ejemplo, puede tener tres orbitales correspondientes am l = -1, 0, +1.
En otras palabras, define los orbitales p x, p y y p z de la subcapa p.
En general, para un l dado, hay 2 l+1 valores posibles para m l.
Y, en una capa principal n, hay n 2 orbitales que se encuentran en ese nivel de energía.
Continuando con el ejemplo anterior:
- Los valores m l de yodo son m l = -4, -3, -2, -1, 0 1, 2, 3, 4.
- Estos corresponden arbitrariamente a los 5s, 5p x, 5p y , 5p z , 4d x 2 -y 2 , 4d z 2, 4d xy , 4d xz y 4d yz orbitales.
Número cuántico magnético de giro (m s)
- El número cuántico magnético de espín solo puede tener un valor de +1/2 o -1/2.
- El valor de 1/2 es el número cuántico de espín, s, que describe el espín del electrón.
Debido al giro del electrón, genera un campo magnético.
- En general, un electrón con am s = + 1/2 se llama electrón alfa, y uno con m s = -1 / 2 se llama electrón beta.
- No hay dos electrones emparejados que puedan tener el mismo valor de espín.
Sin embargo, de estos cuatro números cuánticos,
Bohr postuló que solo el número cuántico principal, n, determina la energía del electrón.
Por lo tanto, el orbital 3s (l = 0) tiene la misma energía que los orbitales 3p (l = 1) y 3d (l = 2), independientemente de la diferencia en los valores l.
Este postulado, sin embargo, es válido sólo para el átomo de hidrógeno de Bohr u otros átomos similares al hidrógeno.
Cuando se trata de sistemas de varios electrones, debemos considerar las interacciones electrón-electrón.
Por lo tanto, el postulado descrito anteriormente se descompone en que:
- La energía del electrón ahora está determinada por el número cuántico principal, n.
- Y el número cuántico del momento angular orbital, l .
Aunque la ecuación de Schrodinger para átomos de muchos electrones es difícil de resolver matemáticamente.
Todavía se puede describir sus estructuras electrónicas a través de configuraciones electrónicas.
